Simple Harmonic Motion(SHM) | Definition, formulas

Hello everyone
Today in this post we are going to study SHM aka Simple Harmonic Motion.

So, let’s start with the introduction.

INTRODUCTION:

Let’s know some important but essential things and terms.

What is a periodic motion?

⇒The motion that is repeated at regular intervals is called a periodic motion.

What is Oscillation?

⇒If a particle with periodic motion travels in the same direction over and over again, its motion is called oscillation. if the particle follows this equation⇒ [F=-A(y-y₀)ⁿ; where n≠1 and n∈odd] then the motion is called oscillatory. if n=1, then motion is S.H.M.

When a particle is said to be in S.H.M?

⇒If the acceleration of an oscillating object is proportional to the displacement of the particle from the equilibrium and is always in the direction of equilibrium, then the motion of that particle is called simple harmonic motion or S.H.M. More generally, if any oscillation follows these equations[Y=Asin(⍵t+ⲫ) or, d²y/dt² +⍵²Y=0], it will be in S.H.M.

Here,

Y=displacement {x always measured from mean position}

A= amplitude{maximum displacement} i.e. |Y_max|=A

ⲫ=Initial phase*

(⍵t+ⲫ)=Phase

⍵= Angular frequency , ⍵=2𝜋⁄T [T = time period]

Now, I think you guys already know these terms like- complete oscillation, time period, frequency, and amplitude. So, I’m not further elaborating on them.

Now,

The graph of the equation Y=Asin⍵t.{which is a sin graph clearly}

Y=Asin⍵t ; |Y_max|=A
Velocity, V=A⍵cos⍵t; |V_max|=⍵A
∴ Acceleration, a= (-A⍵²sin⍵t)= -⍵²Y ; |a_max|=⍵²A

So, from here what we can say?

We can say that-

Displacement and velocity are positive(+ve) whereas acceleration is negative(-ve). This is because acceleration always acts toward the mean position.

*Here in the picture the |Xmax| will be |Ymax|{sorry for the mistake}.

Do you know what is Restoring force?

⇒ Well, when a particle has slightly deviated from its equilibrium position, a force arises which tries to bring the particle back to its equilibrium position. This force is called Restoring force.
So, now see the graphical representation of Y=Asin(⍵t+ⲫ) {as we have already seen the graph of (ⲫ=0) i.e. Y=Asin(⍵t) so I don’t give it here again}-

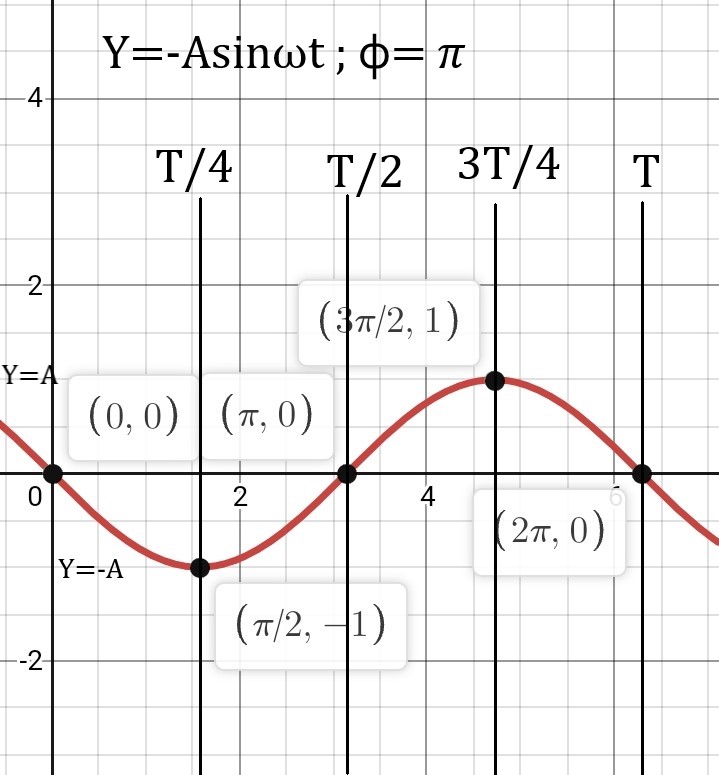
So, from these two graphs we can say that

When ⲫ=𝜋/2, the sine graph becomes a cosine graph and the velocity graph becomes a sine graph. Simple but important!

Similarly for ⲫ=𝜋.

This will be more clear when we study the Generating circle.

Now let’s see some basic mathematical terms/formulas for solving problems.

V=A⍵cos⍵t.

Let’s see what we can derive,

V=A⍵cos⍵t

⇒V= ±⍵√(A²– Y²) {⍵ never become zero or negative}

case 1 x=0 ; V=A⍵ {maximum}

case 2 x=A; V=0 {minimum}

Total energy= m⍵²A²/2

Kinetic Energy=(1/2)m⍵²(A²-x²)

Potential Energy=(1/2)m⍵²x² 

So, from these two graphs what we can say that

When ⲫ=𝜋/2, the sine graph becomes a cosine graph and the velocity graph becomes a sine graph. Simple but important!

Similarly for ⲫ=𝜋.

This will be more clear when we study the Generating circle.

Now let’s see some basic mathematical terms/formulas for solving problems.

V=A⍵cos⍵t.

Let’s see what we can derive,

V=A⍵cos⍵t

⇒V= ±⍵√(A²– Y²) {⍵ never become zero or negative}

case 1 x=0 ; V=A⍵ {maximum}

case 2 x=A; V=0 {minimum}

Total energy= m⍵²A²/2

Kinetic Energy=(1/2)m⍵²(A²-x²)

Potential Energy=(1/2)m⍵²x² 

Now, let’s see-

Generating Circle:

This will help us to understand the motion{oscillation} as well as solve problems. Remember, always measure this circle counterclockwise.

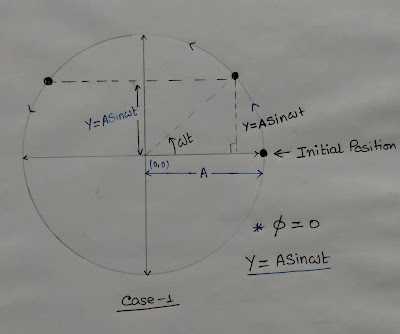
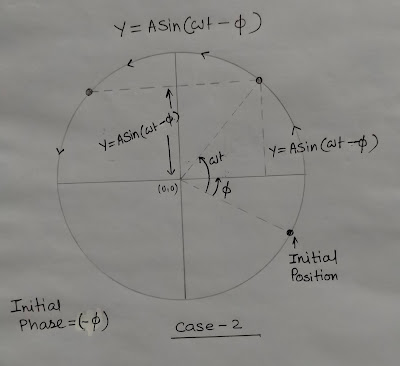
The “generating circle” is also known as the “circle of reference” and the particle is called the “reference particle”.

Hope you can clarify the generating circle from these images. So from these images, we can see-

1. Displacement(Y) is (+ve)positive in the 1st quadrant and 2nd quadrant. (as Y is a sine function)
2. Velocity(v) is positive (+ve) in the 1st and 4th quadrants. (as velocity is a cosine function)
3. Acceleration(a) is positive in the 3^rd and 4^th quadrants. (as acceleration is a sine function with a negative sign )

As you know, the number of full oscillations performed at a single time is called the frequency of simple harmonic motion and is denoted by both ‘n’ and ‘f’. We will use ‘f’ here. We also know that f=1/T.

So, that’s all. Hope this article helps you.

Thank you.

And don’t forget to subscribe to our newsletter to get regular updates.