Everything You Need To Know About Alternating Current

Definition:

An electric current that changes in value and direction over time and passes through a charge cycle at a given time interval is called an ‘Alternating current’.

Ac Dynamo

Definition:

A device that converts the mechanical energy of a rotating conductive coil into electrical energy is called a dynamo.

Working principle:

As the coil ABCD begins to rotate as shown in the fig, the arms intersect the two magnetic field lines AB and CD. This results in electromagnetic induction. Since the motion of the arm AB is downward, the current flows in the direction BA according to Fleming’s right-hand law, whereas for the upward motion of the arm CD, the current flows in the DC direction. So there will be an electric current in the coil in the direction of DCBA. The connection of R₁, R_2, and T₁, T₂ will cause an external circuit of current from T₁ to T₂. This means that in this situation T₁ and T₂ behave like the positive and negative poles of a battery. However, the direction of the flow of this device does not remain unchanged. Whenever the positions of AB and CD arms rotate as a result of the rotation, Fleming’s right-hand rule is applied again and the electric current is obsessed in the direction of ABCD. This causes the current to flow in the outer circuit from T₂ to T₁ i.e. the direction of flow and the polar nature of T₁ and T₂ is reversed.

Expression of AC:

Suppose a rectangular coil rotates in a balanced magnetic field with a right angle angular velocity 𝛚. At some moment(let say, time=t) the angle between the area vector to the coil and the direction of the magnetic field is 𝞱. If magnetic induction =B and the surface area =A then the magnetic flux associated with the coil, 𝜙=BAcos𝞱

Now let us assume that the initial state of the coil is such that the angle between the area vector and the magnetic field of the coil is 𝜶. This angle becomes 𝞱= (𝛚t+𝜶) as a result of the rotation for a period of time t with an angular velocity 𝛚.

Then, 𝜙=BAcos(𝛚t+𝜶)
∴ emf in the coil, e= – d𝜙/dt =𝛚BAsin(𝛚t+𝜶) [∵𝛚BA=e₀] = e₀sin(𝛚t+𝜶)

∴ i = e/R= e₀sin(𝛚t+𝜶)/R= i₀sin(𝛚t+𝜶)
here (𝛚t+𝜶) = phase of AC and 𝜶= period

Average value of Alternating voltage and current:

Let, v=v₀sin𝛚t and its time period t=T then,
V_average = (2v₀/𝛚T)[-cos𝛚t ](0⟶T/2)
∴V_average = 2v₀/𝜋
similarly, I_average = 2i₀/𝜋

RMS value of alternating voltage and current:

V_rms =v₀/√2 and I_rms = i₀/√2
i₀> I_rms >I_average

Why AC is more dangerous than DC?

When power is taken from a 220 v dc line, its voltage is always constant at 220 V. But if power is taken from 220 V alternating current line (220 Vac line), then the voltage also varies according to the nature of the alternating current. Here the RMS voltage of the line = 220 V; Thus, the top value of line – voltage = 220 x √2 = 311 V | For this higher peak, the shock of the alternating current is more dangerous than the shock of the direct current.

P=V_rms I_rms cos𝜃 where cos𝜃 is the power factor of the AC circuit.

DC Motor:

An DC motor is a device that converts electrical energy from an external source into the rotational energy of a coil.

Now, we are going to talk about RLC, CR and LR.

Before jumping directly to these circuits, let’s see the basic circuits.

Before we start learning the circuits, let’s see how we’ve to find out the power consumption in the circuit.

Let, V=V₀sin⍵t and I=I₀sin(⍵t-θ) [where θ= Phase difference & -90°≤θ≤90°]

∴Power consumed in AC circuit,

P=VI=V₀I₀sin⍵t.sin(⍵t-θ)

⇒V₀I₀sin⍵t[sin⍵t.cosθ-cos⍵t.sinθ]

⇒V₀I₀[sin²⍵t.cosθ-cos⍵t.sinθ.sin⍵t]
⇒V₀I₀[sin²⍵t.cosθ-(1/2)sin2⍵t.sinθ]

As the average value of sin²⍵t is 1/2 and the average value of sin2⍵t is 0, that’s why the average power consumption, P_avg
= V₀I₀cosθ/2

Purely Resistive Circuit:

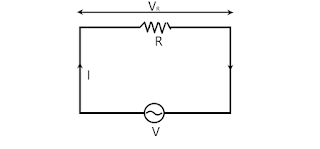
Let, the supply voltage of the circuit is, V=V₀sin⍵t.

As there is no another element except the resistor R, so the voltage across R is also V, i.e. V_R=V₀sin⍵t. —-(1)

Now as per Ohm’s law,
V=IR
⇒I=V/R=V₀sin⍵t/R
⇒I=I₀sin⍵t [where, I₀=V₀/R] —–(2)
Where I₀= Maximum current

From equation (1) &(2) we can clearly say that,

1. Voltage and current are in the same phase. That means the phase difference,θ=0

   
2. As the frequency, f=⍵/2𝜋 and as ⍵ is not changing, so that frequency is also the same.
   Now as θ=0, therefore cosθ=1.

∴ Power consumed in the circuit, P= V₀I₀cosθ/2 = (V₀I₀)/2= {(V₀)/√2}.{(I₀)/√2}

∴ P= V_rmsI_rms.——(1)

Now,

Pure Inductive Circuit:

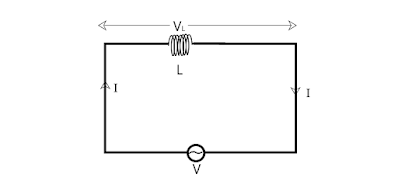
Let, the supply voltage of the circuit is, V=V₀sin⍵t.

As there is no another element except the inductor L, so the voltage across L is also V, i.e. V_L=V₀sin⍵t. —-(1)

If the current I flow through the whole circuit, then the induced emf V_e= -L(dI/dt)

∴ V= V₀sin⍵t-L(dI/dt) ——–(2)
Now as there is no resistance in the circuit, so R=0.
∴V=IR=0
⇒V₀sin⍵t-L(dI/dt)=0
⇒V₀sin⍵t=L(dI/dt)
⇒∫dI= (V₀/L)∫sin⍵tdt
By integrating both sides we get,
I= (V₀/L)(-cos⍵t/⍵)+k
=-(V₀/⍵L)cos⍵t +k

[Here k is a time-independent constant. But in the voltage equation, there is no constant, which means the voltage oscillates symmetrically on both sides of the origin. So that the current generated in the circuit also oscillates symmetrically both sides of the origin. i.e. k=0]

∴ I=V₀cos⍵t/⍵L [where I₀=maximum current=V₀/⍵L]

⇒I=I₀sin(⍵-90°) ——(3)

From (1) &(3) we can easily say that,

Voltage and current are now not in the same phase. Now the phase difference,θ between them is 90°. That’s mean here the current is lagging behind the voltage by the phase difference of 90°.

Now as θ=90°, therefore cosθ=0.

∴ Power consumed in the circuit, P= V₀I₀cosθ/2=0

That’s mean in AC circuit if there is a pure inductor then no power will consume, that’s why this is called wattless current.

Next is-

Purely Capacitive circuit:

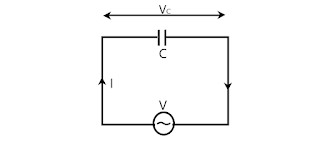
Let, the supply voltage of the circuit is, V=V₀sin⍵t.

As there is no another element except the capacitor C, so the voltage across C is also V, i.e. V_C=V₀sin⍵t. —-(1)

Now if there is a charge Q in the capacitor, then it creates an inverse voltage Q/C.
∴ V= V₀sin⍵t-Q/C ——-(2)
As in the circuit, there is no resistance, so
V=IR=0
⇒V₀sin⍵t-Q/C =0
⇒V₀sin⍵t=Q/C
By differentiating both sides,
⇒⍵V₀cos⍵t=(1/C)dQ/dt=I/C [As I=dQ/dt]
⇒I=C⍵V₀cos⍵t={V₀/(1/⍵C)}sin(⍵t+90°)
⇒I=I₀sin(⍵t+90°) —–(3)
Where maximum current, I₀={V₀/(1/⍵C)}
From (1) & (2) equation we can easily say that,

Voltage and current are now not in the same phase. But now current is no more lagged behind the voltage. Now the phase difference,θ between them is 90°. That’s mean here the current is leading the voltage by the phase difference of 90°.

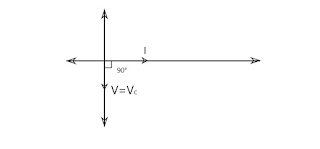
Now the great thing is here, in this case also, the current is wattless.

As θ=90°, therefore cosθ=0.
∴ Power consumed in the circuit, P= V₀I₀cosθ/2=0
That’s mean in the AC circuit if there is a pure conductor then no power will consume, which means the current is wattless.
Now let’s go to the –

LR Circuit:

Here, in this case
Let, the supply voltage of the circuit is, V=V₀sin⍵t.(as usual) ———-(1)

But in this case, as we clearly see that here is an inductor and a resistor in the circuit. So what we can do? See-

If the current I flow through the whole circuit, then the induced emf V_e= -L(dI/dt)
∴ V= V₀sin⍵t-L(dI/dt)
Now according to Ohm’s law,
V=IR
⇒ V₀sin⍵t-L(dI/dt) =IR
⇒V₀sin⍵t=L(dI/dt) +IR ——–(2)
Let, I=I₀sin(⍵t+⍺)
∴ dI/dt = ⍵I₀cos(⍵t+⍺)
Now putting the value of I and dI/dt, we get,
⇒V₀sin⍵t = L⍵I₀cos(⍵t+⍺) + I₀Rsin(⍵t+⍺)
⇒ I₀[L⍵cos(⍵t+⍺) + Rsin(⍵t+⍺)] = V₀sin⍵t

Now let, Z=√{R²+(⍵L)²}[Z is called impudence, and ⍵L=X_L is called the inductive reactance (see below)]
& tanθ = ⍵L/R

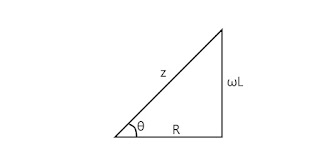
⇒ I₀Z[⍵L/Zcos(⍵t+⍺) + R/Zsin(⍵t+⍺)] = V₀sin⍵t

From the triangle, ⍵L/Z=sinθ and R/Z=cosθ, after substituting we get,
⇒ I₀Z[sinθcos(⍵t+⍺) + cosθsin(⍵t+⍺)] = V₀sin⍵t
⇒ I₀Zsin(⍵t+⍺+θ) = V₀sin⍵t
Comparing both sides we get,
⇒ ⍺+θ =0 ⇒ ⍺=-θ and I₀Z=V₀⇒ I₀ =V₀/Z =V₀/√{R²+(⍵L)²}
∴I=I₀sin(⍵t-θ)=V₀/Z sin(⍵t-θ) ——(3)

From equation (1) and (3) this is clear that,

1. No change occurs in the AC voltage and frequency of the current.
2. The current I is lagging behind the voltage V with a phase difference θ. Where θ= tan^-1( ⍵L/R)

   
3. Whatever a resistance do in a purely resistive circuit, in this circuit the workfunction of Z is the same. Z is called the impedance of the AC circuit. The resistance against the current flowing in the LR circuit is the Impedance of the circuit to that alternating circuit.

∴ Power consumed in the circuit, P= V₀I₀cosθ/2 = (I₀Z)I₀(R/Z) x1/2 = (I₀/√2)²*R

∴P=(I_rms)²R ———-(4)

So, from equation (4) it is clear that in the LR circuit, no power is expended by the pure inductor L, all power is disrupted by the pure resistor R.

CR Circuit:

(As usual, we do)
Let, the supply voltage of the circuit is, V=V₀sin⍵t. ———-(1)

Now if there is a charge Q in the capacitor, then it creates an inverse voltage Q/C.
∴ V= V₀sin⍵t-Q/C

According to Ohm’s law,
V₀sin⍵t-Q/C=IR
⇒ IR + Q/C = V0sin⍵t ———(2)
Suppose that, Q=Q₀sin(⍵t+⍺)
∴ I=dQ/dt=⍵Q₀cos(⍵t+⍺)
Putting the value in equation (2) we get,
⇒⍵RQ₀cos(⍵t+⍺) + (Q₀/C)sin(⍵t+⍺) = V₀sin⍵t
⇒ ⍵Q₀[ Rcos(⍵t+⍺) + 1/C)sin(⍵t+⍺)] = V₀sin⍵t
By simplifying the equation,
⇒⍵Q₀Zsin(⍵t+⍺-θ+90°) = V₀sin⍵t [Here, Z=√{R²+(1/⍵C)²} and 1/⍵C =X_C is called the conductive reactance]
By comparing both sides,
⇒ ⍺-θ+90°=0 ⇒⍺=θ-90°
& ⍵Q₀Z= V₀ ⇒ Q₀ = V₀/Z⍵
Now as I=⍵Q₀cos(⍵t+⍺), we can simplify it. Let’s see what we’ve got after simplifying it,
I=⍵Q₀cos(⍵t+⍺) = V₀/Zcos(⍵t+θ-90°) = I₀sin(⍵t+θ)
∴ I= I₀sin(⍵t+θ) ——-(3)
Where, I₀=V₀/Z= V₀/√{R²+(1/⍵C)²}

From equation (1) and (3) this is clear that,

1. The current I is leading the voltage V by a phase difference θ. Where θ= tan^-1( 1/⍵CR) {The diagrams are the same as the LR circuit.}
2. And similarly, its power consumption is
   P=(I_rms)²R ———-(4)

If you like our site and think that it is a little bit helpful to you then subscribe to our newsletter to get regular updates.

-Thank u😊