Let’s try to understand Gravity

Introduction:

Definition:  The force by that any two particles throughout this universe attract each other is termed Gravity. 

Newton’s Law of Gravitation:

According to Newton, any two particles in the universe attract each other along their connecting straight line. The magnitude of this force is directly proportional to the product of the masses and inversely proportional to the square of the distance between their centres.

Mathematical explanation:

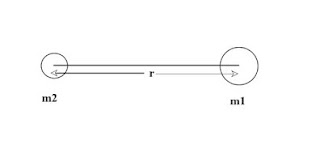
Let, the distance between m₁ and m₂ is r. If they both are attracted by each other by a force F, then acc. to Newton’s law-F∝m₁m₂ {when r is fixed} & F∝1/r² {when m1 and m2 are fixed}

∴ F∝m₁m₂/r² ⇒ F=Gm₁m₂/r² {where G is universal gravitational constant}

Universal Gravitational constant:

Definition: The magnitude of the force for which two unit mass objects attract each other from a unit, distance is called the Gravitational constant(G). 

So, why the Gravitational constant is called Universal?

Well, it is just because of-

According to Newton’s law of gravitation, the force between two objects depends only on their mass and their distance. It does not depend on the condition of the two objects(solid, gas, liquid), chemical composition, temperature, and also the medium between them. So, it is called the Universal Gravitational constant.

Units of G

1.    C.G.S unit = dyn.cm²/g²

2.    S.I unit = N.m²/kg²

3.    F.P.S unit = poundal.ft²/lb²

Values of G

1.    C.G.S=6.67 X 10-8 dyn.cm²/g²

2.    S.I = 6.67 X 10-11 N.m²/kg²

3.    F.P.S = 1.07 X 10-9 poundal.ft²/lb²

What is Gravitational Field?

The space around a mass up to which another mass feels a force of attraction due to gravitation is called the Gravitational field of the former mass.

From fig. 1 if m₁ is the former and  m₂ is the second mass in this definition, then force felt by m₂ by m₁ is the gravitational field of  m₁  i.e. g= Gm₁/r² 

Proof: Acc. to Newton’s law of gravitation we know that  F=Gm₁m₂/r² and from Newton’s 2nd law of motion we can easily say that for this attraction force m₂ will accelerate toward m₁  and experience a force F=m₂.a

Now putting the value of F in the first equation we get

 m₂.a = Gm₁m₂/r² ⇒ a = Gm₁/r² 

now altering ‘a’ with ‘g’ we get g= Gm₁/r² {proved}

[g is also called Gravitational acceleration.]

What is Gravitational Potential?

The amount of work that an external agent has to do to bring an object of a unit mass from an infinite distance to a point in the gravitational field is called the Gravitational potential of that point. 

Gravitational potential, V =∫g.dr = -Gm₁/r {from fig.1}

What is Gravitational Acceleration?

The acceleration of a freely falling object by the effect of a gravitational force is called gravitational acceleration and denoted by ‘g’.

Variation in Gravitational Acceleration:

1.    Variation with altitude: g_h=g(1-2h/R) {in ‘h’ height  from surface of earth of radius R} 

2.    Variation with depth: g_d=g(1-h/R) {in ‘d’ depth from earth’s surface}

3.    Effect of earth’s during motion: g’=(g-𝜔²Rcos²𝜃)

Kepler’s Laws of planetary motion

In the early 1600s, Johannes Kepler proposed three laws of planetary motion. Kepler was able to summarize the carefully collected data of his mentor – Tycho Brahe – with three statements that described the motion of planets in a sun-centred solar system. Kepler’s efforts to explain the underlying reasons for such motions are no longer accepted; nonetheless, the actual laws themselves are still considered an accurate description of the motion of any planet and any satellite.

1.    First Law: Each planet orbits the Sun in an elliptical orbit and the Sun is in the focus of that ellipse.

2.    Second law: The line connecting the Sun and any planet crosses equal areas in equal time. This law is basically the principle of conservation of angular momentum.

3.    The square of the time period of any planet (time of revolution of the planet around the sun,) is proportional to the cube of the semi-major axis of the elliptical orbit of that planet i.e T²∝ R³.